基于DEMSLab 的气固两相弯头磨损的仿真方法
01 前言 当流体携带固体颗粒撞击固体表面时,在固体表面会产生材料损失,称之为磨损。磨损现象存在于很多工业领域,例如化工、采矿、能源和农业等。具体而言,石油和天然气工业中的设备经常会发生磨损,比如在石油工业中,管件的快速磨损是一个主要问题。其中弯头用于流速转向是管道系统必不可少的组成部分。此外弯头发生的泄漏会引起污染等情况的发生,会带来巨大的经济损失。总的来说,我们有两种可能的方法来控制磨损,一是选择合理的工作条件,二是选择抗磨损材料或者采用表面喷涂增强表面磨损特性。但是如果我们不知道管道中的损失分布,则控制工作则无法执行。因此,准确地预测磨损程度、磨损区域对于防止弯头失效至关重要。实际上,许多行业都致力于开发可靠的数值仿真工具,磨损模型的准确性和粒子运动的计算对磨损的数值仿真至关重要。 CFD-DPM(计算流体动力学离散相模型)和CFD-DEM(计算流体动力学离散元方法)是两种微尺度下弯头粒子运动的计算模型。CFD-DPM是流固两相流的一种广泛使用的方法,但是,因为CFD-DPM方法建立在忽略颗粒之间相互作用的基本假设之上,因此CFD-DPM模型仅适用于稀相流。这也是在多数密相流工业应用中很难仿真的原因,直到CFD-DEM方法开发成功,密相流的仿真也成为可能。DEM可以模拟粒子运动,例如分子运动,并且可以计算粒子之间的相互作用。因此,该方法具有可用于研究高浓度颗粒流的优点。目前,CFD-DEM已成功应用于与管道系统和腐蚀相关的各个领域。有相当多的研究者使用CFD-DEM方法研究了进料管的磨损,并获得了与实验具有相当一致性的计算结果,并获得了一些无法使用CFD-DPM提取的结果。 除了颗粒的曳力模型,颗粒的磨损模型对于准确预测磨损也是必不可少的,到目前为止,研究者已经根据实验研究方法对磨损机理进行了各种分析,提出了几种类型的磨损模型,比如Finnie韧性磨损模型、Bitter的韧性和脆性综合磨损模型、Neilson和Gilchrist韧性和脆性综合磨损模型,Sheldon和Finnie的90°脆性磨损模型等。Finnie的韧性磨损模型已成功应用于CFD-DEM 。但是,根据Finnie理论的局限性,该模型似乎不适用于稠密条件。最近,由Ashrafizadeh等人首先将结合剪切冲击能的磨损模型应用于DEM模拟。该模型可用于稀流和浓流,因为磨损是根据冲击能量计算得出的。Ashrafizadeh等人预测的侵蚀与来自相应实验的数据进行了比较。结果表明,腐蚀速率和剪切冲击能之间存在定性线性关系。尽管Ashrafizadeh模型不是定量的数学模型,无法准确预测侵蚀速率,但报告的结果表明,将侵蚀和剪切冲击能结合起来是一种新方法。在DEMSLab团队之前的研究中,在Ashrafizadeh的工作的基础上,基于DEM提出了定量的磨损模型SIEM(剪切冲击能量模型)。事实证明,DEM的颗粒腐蚀模型SIEM可以准确预测磨料腐蚀。 本次研究中,基于非球形颗粒离散元软件DEMSLab,采用CFD-DEM方法进行颗粒流计算,考虑颗粒-颗粒和颗粒-壁面相互作用,使用磨损模型SIEM预测了由颗粒撞击引起的弯头磨损。通过将模拟结果与来自模拟系统的数据进行比较,验证了该方法在稀疏条件下的准确性。因为CFD-DEM耦合方法和磨损模型都可以在稠密条件下应用,所以文中还研究了颗粒浓度对弯头磨损的影响。此外,还研究了摩擦系数、恢复系数和弹簧刚度系数对腐蚀的影响。 02 DEMSLab软件介绍 DEMSLab软件是DEMSLab公司基于离散单元法(DEM)开发的针对颗粒系统进行模拟的大型商用软件。DEMSLab以领先的非球形离散单元技术为核心,致力于工业级的大规模颗粒体系的模拟。通过精确模拟设备内的复杂颗粒运动、传热、及颗粒-流体、颗粒-设备间的复杂作用,DEMSLab可帮助企业降低设备的能耗及损耗,提高设备的运行效率。 DEMSLab软件包含前处理器、求解器及后处理器三大部分。前处理器可进行设备的复杂几何造型,颗粒生成器可根据该几何结构自动生成所需要的颗粒。求解器通过OpenMP技术进行了并行设计,可对10,000,000颗粒规模的球形及非球形颗粒体系进行动态模拟,支持复杂结构及运动(振动、旋转、移动等)边界条件、周期性(包含Lees-Edwards)边界条件等,具备用户自定义接口,支持用户自定义开发,可与常用商用及开源CFD软件(如Fluent等)进行双向耦合,以求解两相流动问题。后处理器采用Open GL编程技术设计,可实时显示颗粒体系的运动过程,同时可对任意时刻的微观受力情况进行分析。软件技术特点如下: (1)领先的非球形颗粒模型 DEMSLab软件拥有领先的非球形颗粒模型构建功能,同时采用了三大类颗粒形状模型,可以精确地描述任意真实颗粒形状。 第一类是球类颗粒形状模型(Sphere-basedmodel),包括球形模型(Spheremodel)、组合球模型(Multi-spheremodel)、粘结球模型(Bonded-sphere model)、以及微滴模型(Droplet model); 第二类是超椭球类颗粒形状模型(Super-ellipsoid-based model),包括超椭球模型(Super-ellipsoid model)和组合超椭球模型(Multi-super-ellipsoid model); 第三类是多面体类模型(Polyhedron-based model),包括凸多面体模型(Convexpolyhedron model)和凹多面体模型(Concavepolyhedron model)。 用户可以根据需要选用上述颗粒形状模型,对所需解决的问题进行快速、准确的数值仿真。需要说明的是上述三类颗粒模型可以在同一个项目中同时使用,因此用户可以根据需要选择不同的颗粒形状模型,并应用在同一个工程问题中。
DEMSLab软件支持的颗粒模型 (2)具备三大通用模块 DEMSLab软件拥有以下三大模块:①前处理器、②求解器、③后处理器。 (3)支持通用CAD软件建模 DEMSLab软件支持通用CAD软件(例如UGNX、Pro/E、SolidWorks CATIA等)建模或者ANSYS Fluent的网格文件(可以由ANSYSFluent的前处理器生成,比如ANSYS ICEM CFD或Gambit软件)。DEMSLab软件中设备几何文件(mesh文件)可以通过通用CAD软件输出的stl文件或ANSYS Fluent的网格文件(msh文件)进行转换并导入。 (4)并行化求解 DEMSLab软件采用OpenMP技术进行程序设计,可在拥有多核处理器的共享内存服务器或个人电脑上高效运行。DEMSLab软件可在一台具备32GB内存的计算机上对10,000,000颗粒规模的球形及非球形颗粒体系进行动态模拟,其计算速度取决于计算机上处理器的总核数及时钟频率。 (5)支持复杂边界运动 DEMSLab软件支持复杂结构及运动(振动、旋转、移动等)边界条件、周期性(包含Lees-Edwards)边界条件等,也可以用户自定义边界的复杂运动。 (6)支持用户自定义开发 DEMSLab软件提供总数超过200个的API函数用于用户开发自定义函数(UserCFunctions)。通过UserCFunctions,用户可以自定义更为复杂的边界运动、接触力模型、颗粒参数、破碎模型、曳力模型等。 (7)支持与其它CAE软件耦合求解 通过User C Functions,DEMSLab软件可以与通用CFD软件(比如ANSYSFluent)、FEM软件(比如ANSYS Structure)及MBD软件(比如Adams)进行耦合求解。 (8)先进的后处理器 后处理器采用OpenGL编程技术设计,可快速高效地实时显示颗粒体系的运动过程,同时可对任意时刻的微观受力情况进行分析。 (9)完善的帮助文档及大量的案例教程 DEMSLab软件提供数千页的帮助文档及数十个实际的案例教程,用户可通过帮助文档和教程快速掌握DEMSLab软件的使用。
03 数学模型及算法 3.1 颗粒模型 颗粒的平动和转动可以用牛顿第二定律进行计算,如下式:
其中Fc是接触力、Fd是流体阻力、FIS是Saffman升力、FIM是Magnus升力、Fb是浮力、m是质量、I是颗粒的转动惯量、dv/dt是颗粒的平移加速度、g是当地重力加速度、dω/ dt是颗粒的角加速度、Tc是接触扭矩、Tf是流体引起的扭矩。其中接触力Fc可以使用下式来计算:
其中,Fc,n是法向力、Fc,t是切向力。 使用Cundall和Strack提出的线性弹簧-阻尼器模型来计算两个粒子之间的接触力Fc,n和Fc,t:
其中δn是粒子之间的法向变形,δt是切向变形,Vn和Vt分别是粒子之间的法向和切向相对速度。kn和kt分别代表弹簧的法向和切向刚度,其中ηn和ηt分别代表弹簧的法向和切向阻尼系数。根据Ting和Corkum给出的方程,一旦知道恢复系数,就可以得到阻尼系数。对于切向接触力,当接触力的两个分量都满足等式中所示的条件时,可用库仑摩擦模型计算:
同时,切向接触力可以用下式计算:
这里fs是滑动摩擦系数。 模型中接触扭矩Tc等于接触力产生的扭矩Tt.
同时,切向接触扭矩可以用下式进行计算:
其中n代表法向,r代表径向。 3.2 磨损模型 根据Ashrafizadeh先前的研究,根据撞击过程中的剪切冲击能,开发了一个颗粒尺度的磨损模型SIEM。在此模型中,在碰撞过程中被颗粒去除的材料的体积表示为:
其中p表示被撞击表面的塑性流动压力;通常根据Finnie等人的实验数据,p约为hv的1至5倍,hv是目标表面的维氏硬度。根据Finnie等人收集的铝的实验数据,假定p为维氏硬度的4.2倍。EShear是在DEM模拟中壁在撞击过程中从粒子获得的剪切冲击能量,可以在DEM中使用以下公式计算:
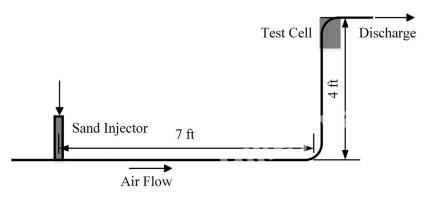
其中,Fc,t表示粒子撞击表面时接触力的切向分量,Vt表示相对速度的切向分量;冲击从t0开始,到t结束。剪切冲击能量仅在Fc,t*Vt < 0和Fc,t*V<0时才在冲击过程中积累,因为剪切冲击能仅在此条件下才转换为磨损。最后,对于多颗粒情况,通过将每次操作所截取的材料体积相加即可得出磨损量。与Finnie的磨损模型相比,该新模型既适用于稠密颗粒流,也适用于稀颗粒流,因为磨损是根据剪切冲击能以及任何冲击类型的剪切冲击能计算得出的(包括直接冲击,非直接冲击和滑动)最终可以通过使用DEM仿真以相同的方式获得。另外,由于不需要其他复杂的算法,因此SIEM简单易用,可应用于DEM。 3.3 解决方案和仿真条件介绍 对于连续相,在FLUENT软件中采用SIMPLEC方法求解气流的控制方程。控制方程的对流项采用QUICK微分方案,并且采用基于压力的隐式积分方法来计算流体的运动。对于固体颗粒相,通过用户定义函数(UDF)将自行开发的DEM代码合并到FLUENT中,并且在CFD和DEM之间采用了耦合方案。显式时间积分方法用于计算DEM中粒子的运动。根据Ting和Corkum的建议,将时间步长设置为小于临界值。 Chen等人的实验结果被应用于验证模型和本文中使用的方法。 实验的设置如图1所示。空气被用作连续相,并由空气压缩机以150 ft / s(45.72 m / s)的速度供应到管道,并注入了沙子 以40磅/天(约0.000208千克/秒)的质量流量连续地进入管道。弯管在测试室中,流体垂直向上流入并水平排出。
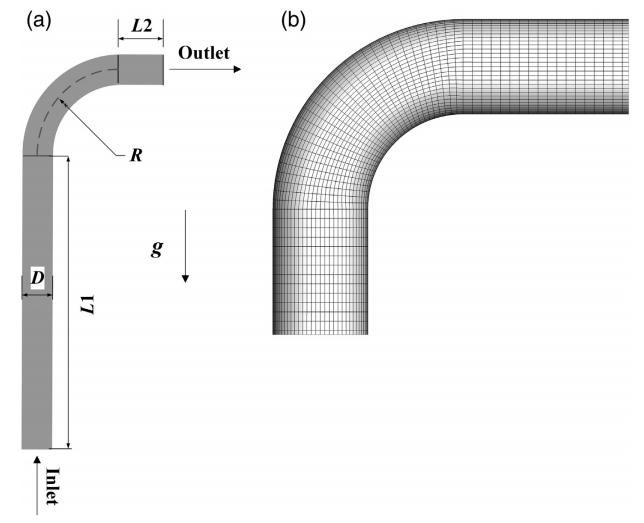
图1 试验装置示意图 基于实验进行了对照仿真。但是如果对整个试验进行DEM模拟,则大量的粒子需要极大的计算资源。因此,仅模拟了实验的最后一部分。模拟部分包含垂直管,测试弯头和水平管,如图2(a)所示。图2(b)显示了仿真中弯管的CFD网格。
图2 计算域及网格 根据实验,在垂直管的入口以0.000208 kg / s的均匀流速提供颗粒。模拟中的入口速度曲线简化为均匀的。沿流动方向的平均速度设置为2.5 m/s,三个速度分量的均方根值为1.6 m/s。湍流的边界条件是按照Ferziger和Peric 的描述设置的。基于入口处的雷诺数和估计的湍流长度尺度,湍流动能k为4.77 m2/s2,湍流耗散率ε为963 m2/s2。在模拟中,在给定当前入口边界条件的情况下,粒子运动在到达弯头之前达到了准稳态。在DEM中,时间步长为5×10-7s,对于CFD,时间步长为5×10-6s,每种情况下的模拟实时运行10 s。除了基于实验的模拟(可以称为“标准模拟案例”)之外,还进行了其他一些模拟来研究颗粒浓度以及摩擦系数,恢复系数的影响,弹簧刚度系数。在较密集的情况下,粒子的浓度设置为标准情况下的浓度的10倍,100倍和1000倍,分别为0.00208 kg / s,0.0208 kg / s和0.208 kg / s。在最密集的模拟情况下,流域中的粒子总数超过一百万。稀释时的颗粒-颗粒摩擦系数和颗粒-壁摩擦系数分别设置为0.1、0.2、0.3、0.4、0.5和0.6以测试摩擦效果。为了研究阻尼的影响,将颗粒-颗粒以及颗粒壁的恢复系数设置为0.8、0.85、0.9和0.95。法向弹簧刚度系数设置为2100 N / m,7000 N / m,21,000 N / m,切向弹簧刚度系数设置为600 N / m,2000 N / m和6000 N / m m测试弹簧刚度的影响。 表1中列出了仿真参数的详细信息。所有的计算都在两个月之内使用具有两个Intel Xeon六核2.60 GHz CPU和16.0 GB RAM的64位计算机完成的。
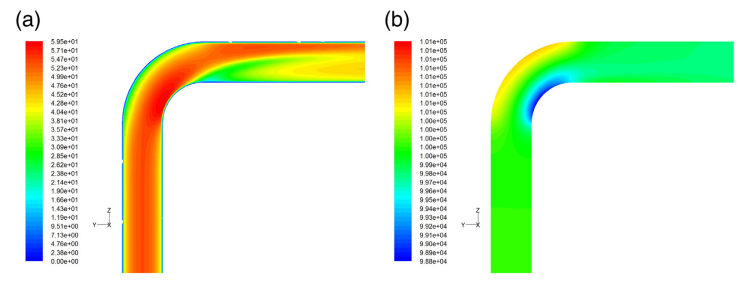
04 结果与讨论 4.1 空气流动 空气流动对粒子运动有重要影响。图3(a)和(b)使用CFD模拟管道中的纯流体,说明了Y-Z平面中设备内部流体的速度场和压力场。在速度场中,流速在垂直管中均匀分布。在弯管出口附近存在低流速区域,在该区域中气流不均匀,并且存在低速区。原因是,当空气流入弯头时,压力的分布在离心力的作用下发生变化,在弯头的附近可以找到最大的压力和最低的压力,如图3(b)所示。由于当前研究中的颗粒浓度不高,因此双向耦合模拟的模拟结果与纯空气的模拟结果相似。
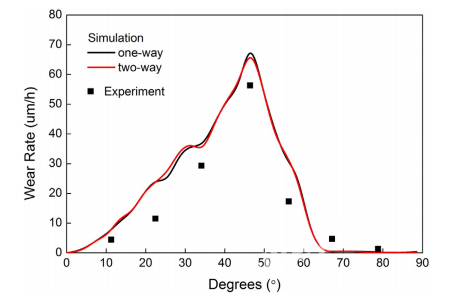
图3 速度和压力云图 4.2 使用单向和双向耦合验证模型 在标准模拟情况下,使用单向和双向耦合方法来计算弯管的磨损。模拟的条件与实验的条件基本相同,并且以与实验相同的方式提取沿肘部外弓中心线的磨损数据。将结果与实验数据进行比较,以验证数学模型和数值方法。图4显示了在从入口(0°)到出口(90°)沿肘部拱门中心的预测磨损曲线与实验数据之间的比较。可以清楚地看到,仿真结果与实验数据基本吻合,这表明当前研究的模型和方法对于预测磨损是有效的。此外,单向和双向耦合方法之间的差异很小,这表明在气固流稀化条件下,耦合方法对弯头的磨损影响很小。从入口(0°)到出口(90°),沿外凸中心线的磨损率首先增加,然后迅速减少。当度数在40–50°的范围内时,磨损率会在0–40°的范围内增加到最大值。然后,磨损率在50–70°的范围内显着降低,而在70–90°的范围内几乎没有磨损。这些现象的原因是,不同区域接收到的剪切冲击能不同。由于冲击角小,肘部入口附近的外腔内壁几乎没有剪切冲击能。然后,剪切冲击能量随位置的增加而迅速增加,直到该位置达到临界值,此后获得的剪切冲击能量较小。在最大位置处,颗粒的冲击角太大,并且在该位置处获得的剪切冲击能量很小。
图 4 磨损率曲线 (颗粒流率为0.000208kg/s,摩擦系数为0.3,恢复系数为0.9)
图 5 磨损率曲线 (颗粒流率为0.00208kg/s,摩擦系数为0.3,恢复系数为0.9)
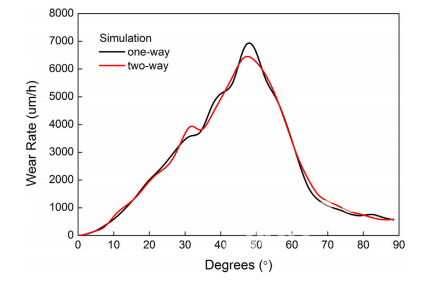
图 6 磨损率曲线
(颗粒流率为0.0208kg/s,摩擦系数为0.3,恢复系数为0.9)
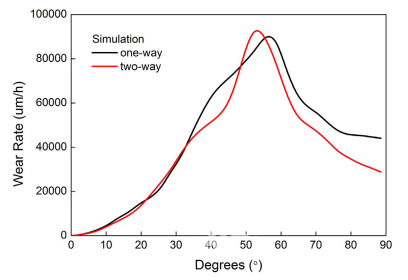
图 7 磨损率曲线 (颗粒流率为0.208kg/s,摩擦系数为0.3,恢复系数为0.9) 4.3 高颗粒浓度下的模拟结果 除上述标准模拟情况外,还进行了其他一些模拟研究,以研究颗粒浓度和耦合方法对肘部磨损的影响。将模拟中的粒子浓度设置为实验浓度的10倍,100倍和1000倍。图5,图6和图7显示了两种耦合方法对不同浓度的情况给出的模拟结果的比较。显然,除了最密集的情况外,单向耦合方法的仿真结果与双向耦合方法的相应结果基本相同。当浓度为实验浓度的1000倍时,使用双向耦合方法获得的磨损略有增加。如图7所示,比在最大出口位置处使用单向耦合方法获得的结果要低。为了直观地描述耦合方法的效果,在图5和图6中示出了使用两种耦合方法获得的磨损图片,参见图8和9。显然,使用两种耦合方法获得的磨损云图非常相似。对于三种较低浓度的情况,磨损模式和磨损率值基本上彼此相同。但是,对于浓度最高为实验浓度1000倍的最稠密情况,使用两种耦合方法获得的磨损存在一定差异。单向耦合模拟结果的严重磨损面积略大于双向耦合模拟的结果。图9说明了使用两种耦合方法获得的弯头中的粒子运动或位置。当粒子浓度较低时,使用单向耦合方法获得的粒子运动或位置也与从双向耦合方法获得的相应结果基本相同。对于最密集的情况,存在一些差异。由于在使用双向耦合方法时会考虑从粒子到气体的阻力,因此在外孔内壁附近的气体速度小于使用单向耦合方法模拟的速度。因此,弯头内壁附近的粒子速度也较小,这导致较少的磨损量。实际上,即使对于当前研究中最稠密的情况,固体部分也仅约占1%,仍被归类为稀薄的气固流。从模拟结果可以看出,当固含量为<1%时,可以使用单向耦合方法预测管道中的腐蚀。
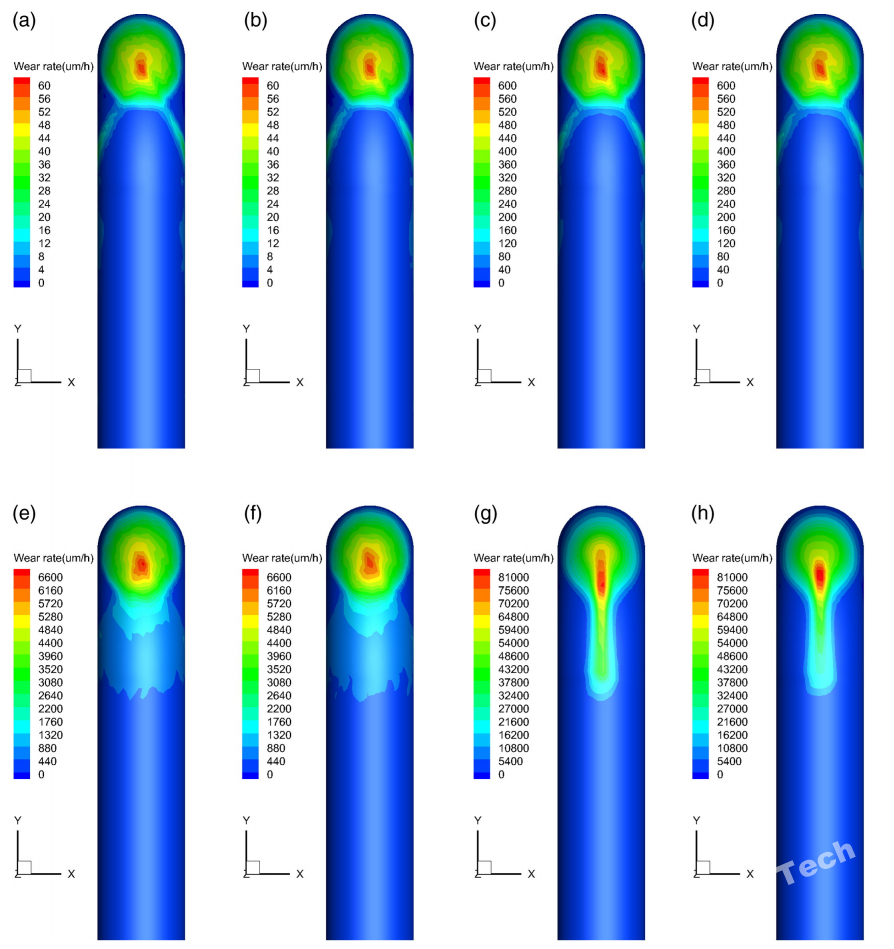
图 8 磨损云图视图一 (单向和双向耦合磨损对比,颗粒流率(a)和(b)0.000208kg/s, (c)and(d)0.00208kg/s,(e)和(f)0.0208 kg/s,(g)and(h)0.208 kg/s, 摩擦系数为0.3,恢复系数为0.9)
图 9 磨损云图视图二 (单向和双向耦合磨损对比,颗粒流率(a)和(b)0.000208kg/s, (c)and(d)0.00208kg/s,(e)和(f)0.0208 kg/s,(g)and(h)0.208 kg/s,摩擦系数为0.3,恢复系数为0.9)
05 结论 基于非球形颗粒离散元软件DEMSLab,采用CFD-DEM耦合方法以及SIEM磨损模型,使用数值模拟预测了弯管磨损现象。从相应实验中提取的数据用于验证数学模型和数值方法。还研究了颗粒浓度,摩擦系数,恢复系数和弹簧刚度系数对肘部磨损的影响。从结果可以得出以下结论: (1)由于仿真结果与实验结果基本吻合,因此模型和仿真方法的准确性都很好。本文提出的方法对于预测肘部的磨损是有效的。 (2)当固含量为<1%时,单向耦合方法和双向耦合方法之间的差异很小,并且单向耦合方法也足够准确可以预测肘部的磨损。但是,对于固体成分为>1%的情况,应使用双向耦合法。 (3)研究浓度对肘部磨损的影响,并且当前模型可用于高浓度气固流动,因为它包含了颗粒之间的接触。结果表明,颗粒浓度在肘部磨损中起主要作用。随着颗粒流速的增加,弯管内壁的磨损率明显在70–90°范围内增加。当流量为c=0.208 kg/s时,水平管中会出现长而窄的磨损区,这是由于壁附近形成的颗粒层滑动引起的。 (4)与浓度不同,摩擦系数仅对肘部侵蚀有轻微影响,而当颗粒浓度较低时,恢复系数和弹簧刚度几乎没有影响。 更多关于DEMSLab软件详情,请看下方
颗粒系统仿真技术交流QQ群:178717288 DEMSLab 视频教程、应用案例集:edu.yanfabu.com/course/explore/demslab DEMSLab 软件试用申请:bbs.yanfabu.com/plugin.php?id=yfb_form&mod=view&form_id=135 |

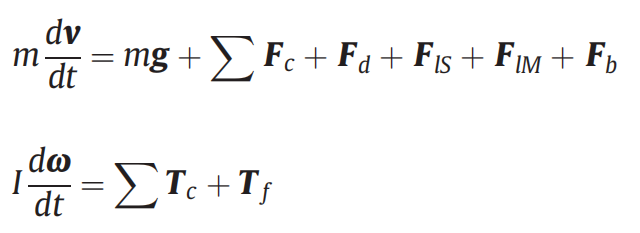
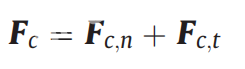


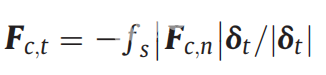
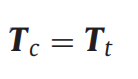

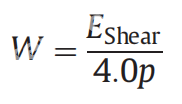
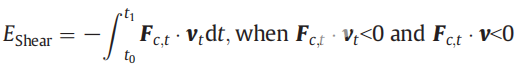








 360网站安全检测平台
360网站安全检测平台